While Tony is out of the office on business, I have once again seized the opportunity to steal a spot on the blog page. I was only supposed to respond to a couple of comments on the blog, so I’d better get this one out quick before he gets back and catches me red handed!
It’s been a while since we’ve had a real nuts and bolts engineering entry in the blog and thanks to Mr. Garford-Tull for providing some comments to previous blog entries. I’ve been inspired to write a technical entry about a few of the more complex issues surrounding thermal effects. Ostensibly his question was related to painting a prop to alter its thermal response – but it also touched upon ideas about differential temperature change. I didn’t want to give a short response in the comments sections as there was far too much meat on that question and I thought it deserved a whole page to itself and get our teeth properly stuck into it.
The question I’m seeking to answer, in short, is: “what if the top of the props gets hotter than the bottom?” First I’m going to go back to a well-used example from a site in Scandinavia. In the winter the air was cold, but generally the sky was clear. So air temperature had a smaller impact and direct radiated heat from the sun was the main driver of prop temperature. In this case we actually measured a variance in temperature of about three degrees between the sensors on the top and bottom of the tube. So indeed, in certain circumstances, there can be a temperature differential. But we also have examples where the direct light of the sun isn’t the driving factor and the air heats and cools the whole prop pretty much uniformly
There have only been a handful of times when we have monitored a single prop in multiple locations to test this differential effect – perhaps 5 times from over 70 monitored sites – so please don’t draw any firm conclusions from what I’m writing. But let’s stick with the first example of 3 degrees for now as it is the best primary data I have.
The question was asked about differential temperature, but really we are interested in the differential stress that this leads to. Let’s work with the idea of 3 degrees Celsius from the example above on a purely steel prop (one can put this into context with a hydraulic prop, but a uniform prop of a single material makes the algebra much easier!). Putting the temperature in terms of stress is fairly easy, since we know what the Young modulus and linear thermal expansion of steel are. To keep things in line with current practice we’ll also include that β factor.
E = 210,000 N/mm²
α = 12 x 10-6 /°C
β = 0.4
so the difference in stress between the top and bottom of the prop would be E x α x β = 1.008 N/mm²/°C
for our case of 3 degrees = 3 N/mm²
Now I want to talk about the overall stress due to thermal effects as a whole. I’m not going to go into too much detail, but taking 30 degrees Celsius on a 610x12.7 CHS (same tube as our MP250s) as an example you’d get a thermal load of about 720kN. This gives a stress in the 610 tube of 30 N/mm² - which makes sense as we are comparing 3 degrees with 30 degrees. By comparison, the differential effect is small compared to the overall stress from thermal effects.
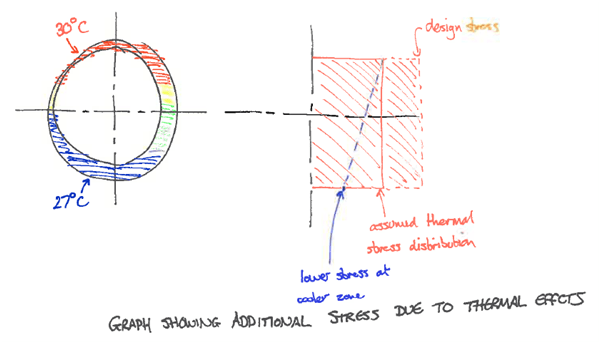
Take a look at the (sorry it’s very crude) diagram above. This small differential could explained away by saying that the differential stress is already included in the assumption of 30 degrees Celsius. That value is picked based on the worst case temperature and the fact that there is a little less stress at the bottom of the prop doesn’t harm anything, so it can just be ignored. Even if the differential isn’t covered in the 30 degrees – it certainly is covered by the partial factor which multiplies the force/stress by 1.5 and takes into account such minor uncertainties.
But looking more closely at it, you might be correct to say that this stress distribution looks just like an average temperature effect of 28.5 degrees Celsius applied with a slight eccentricity. This is looking a lot like the Groundforce method of prop verification! You see, we almost always include a certain amount of eccentricity when we verify the resistance of our props. This induces a small (or sometimes not so small!) moment into the prop.
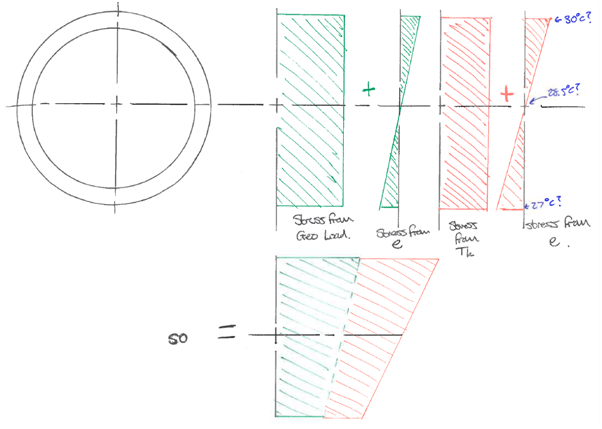
If you think about it too much, you might argue that this eccentricity should really only apply to external forces like the earth pressure to represent the possibility of the force not acting through the exact centre of the prop. But we have always taken the view that it should also be applied to the thermal effects (an internally generated force) and this argument over differential temperature effects is one of the reasons why we do that. You end up with a stress distribution like the one shown above.
So after all that, I suppose the final answer is: Yes, differential temperature effects can occur. But given a CHS prop, we tackle the issue with eccentricity. And by assuming that this moment due to eccentricity acts in the vertical axis, stacking with the moment effects of self-weight; you will always be verifying against the most onerous condition and therefore produce a safe design.
As far a painting the props white… it certainly won’t hurt, but honestly, I don’t have much experience of any props that aren’t painted yellow. But as the lightest primary colour, I’m certain that a yellow prop will perform better than a prop that is Red or Blue!!
Comments
Blog post currently doesn't have any comments.