For those of you who have been on tenterhooks since the basic principals of hydraulic struts entry back in March, your wait is finally over as in this edition I intend to take it one step further and delve into more advanced workings of hydraulic struts. For those who have only been reading the blog to keep updated on the general goings on within the department and progress in the 3 peaks challenge, you may want to give this one a miss!
I ended the last session explaining how the pressure in the struts increases to what is known as an “installation pressure” as it is pumped out between two opposite walls that will not move very much. Once the strut has been installed correctly and the excavation commences, the ground that is being retained applies load onto the strut. This high strength strut is designed to resist this load as you would expect, and it acts as a support, preventing the sides of the excavation from collapsing. This load is transferred along the entire length of the strut, through the hydraulic ram and into the ground at the opposite side of the excavation, keeping everything in equilibrium.
Ignore most of this for a moment and just consider the load going through the hydraulic ram. It travels along the piston rod, into the piston and finally through the column of hydraulic fluid as shown;
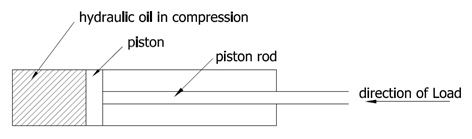
It is a common misconception that a liquid (in this case hydraulic fluid) is incompressible. In reality when they are subjected to load they are subject to a small amount of compression, known as “squash”.
Before I go any further, I must clarify that this type of compression is common for all types of material (including steel) but the extent to which this happens varies depending on what is known as the “modulus of elasticity” , Youngs Modulus” or “E value” of the material. For comparative purposes here are some useful values;
Esteel = 210 000 N/mm2
Eshyd = 160 000 N/mm2
To give you some idea of what this means, the lower the E value, the more compressible the material is. The value of Ehyd given above has been derived from data that Groundforce has obtained through a series of rigorous tests. The tests simply involved positioning a strut in a test rig, applying load to it and measuring the subsequent amount of “squash”. We then simply put the results into the following formula to come up with the modulus of elasticity of hydraulic props;
E = stress = σ = F / A
strain ε δL /L0,
Simple!
If you`re anything like me, you’re probably thinking to yourself one of two things…….. is their any benefit of a more compressible strut and how can you reduce the amount of “squash” when the strut is subject to load?
Well let’s answer one at a time, firstly the benefits. You may or may not be aware but a general rule is that a stiffer support (higher E value) tends to attract more load than a less stiff one. So, if you had two identical excavations, one with a structural steel frame and one with a hydraulic system, the steel frame would be more heavily loaded. This means that in some (not all) situations, it may be possible to use a smaller hydraulic frame than a steel one as the load it needs to resist is not as high.
To reduce the amount of “squash” in a strut, you need to look into a process that we refer to as pre-stressing. This is when the anticipated load (calculated by design) is put into system at the time it is installed and before any excavation has taken place. By doing this you are reducing any additional load that you would expect on the frame as the excavation proceeds and it is this additional load that will cause the “squash”. It is possible to induce a relatively accurate amount of pre-stress (or pre-load) into the struts by simply increasing the installation pressure accordingly. Knowing that pressure is equal to force divided by area, we can use this linear relationship and the extract from our technical file below, to determine the actual installation pressure required for a specific load in any strut type.
| Strut Type |
Strut Capacity* (kN) |
Load/1000 psi (69 Bar) Tonnes/kN |
| MP50 |
530 |
8.6/86 |
| HSK80 |
800 |
13.8/138 |
| MP125 |
1250 |
21.5/215 |
| HSK150 |
1500 |
34/340 |
| MP250 |
2500 |
44.2/442 |
*Using non-standard pumps it is possible to achieve a pre-stressin a single prop of approximately 80% of its axial capacity. Refer to technical services for more information.
Comments
Blog post currently doesn't have any comments.